منطق کامپیوتر چیست؟ در کامپیوتر همه چیز به صورت صفر و یک کار میکند، یعنی همه چیز یا صفر است یا یک، یا روشن است یا خاموش. منطق کامپیوتر یکی از بنیادی ترین شاخه های علم کامپیوتر است که، به بررسی اصول استدلال، تفکر منطقی و نحوه ی پردازش اطلاعات توسط ماشین ها میپردازد. این علم پایه گذار طراحی مدار های دیجیتال، الگوریتم ها و زبان های برنامه نویسی است.
در منطق کامپیوتر مفاهیمی مثل: گزاره، عملگر های منطقی، جدول ارزش و استنتاج مورد مطالعه قرار میگیرد. هدف اصلی ان یافتن روش هایی دقیق و ریاضی شکل برای تصمیم گیری و حل مسئله است. منطق نقش مهمی در هوش مصنوعی و سیستم های خبره دارد، چون امکان استدلال خودکار را فراهم میکند. در کل منطق کامپیوتر پلی میان تفکر انسانی و عملکرد ماشین به شمار میرود.
بیت چیست؟
در منطق کامپیوتر هر صفر یا یک در کامپیوتر یک بیت است. یعنی اگر هشت خانه داشته باشیم در هر خانه یا صفر قرار میگیرد یا یک، که به هر یک از این خانه ها یک بیت میگویند. بیت bit کوتاه شده عبارت binary Digit به معنی رقم دو دویی میباشد و کوچک ترین واحد اندازه گیری داده در کامپیوتر به شمار میرود.
هر بیت میتواند فقط یکی از دو مقدار ممکن را داشته باشد: 0 یا 1 . این دو مقدار نشان دهنده ی دو حالت منطقی هستند، معمولا به صورت 0 = خاموش، نادرست ،False و 1 = روشن، درست True است. تمام داده هایی که در کامپیوتر ذخیره یا پردازش میشوند از متن و تصویر گرفته تا صدا و ویدیو در نهایت به ترکیبی از بیت ها تبدیل میشوند. 8 بیت برابر با یک بایت Byte است که میتواند 256 حالت مختلف از 0 تا 255 را نشان دهد.
بایت چیست؟
در منطق کامپیوتر هر هشت بیت یک بایت است. بایت Byte واحدی از داده در کامپیوتر است که از 8 بیت تشکیل میشود. هر بایت میتواند 256 مقدار مختلف را نمایش دهد. بایت ها برای نمایش کاراکتر ها، اعداد، تصاویر و داده های مختلف در سیستم های دیجیتال به کار میروند. یک حرف مثل آ یا ب معمولا با یک بایت نمایش داده میشود.
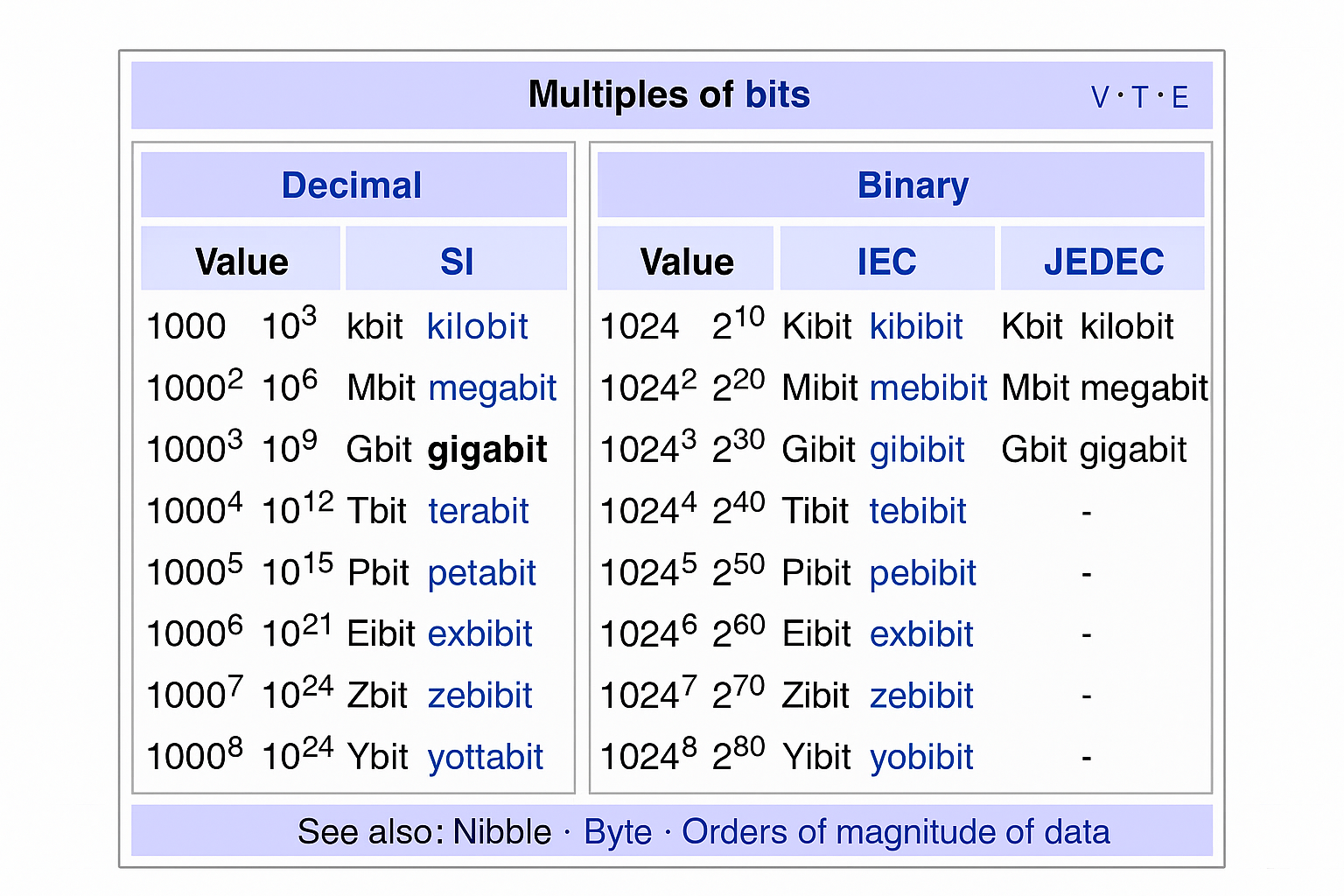
اندازه ی فایل ها حافظه و ظرفیت ذخیره سازی دستگاه ها نیز با بایت و مضارب ان با کیلو بایت، مگا بایت، گیگا بایت و… سنجیده میشود. بایت واحد اصلی ذخیره سازی اطلاعات در کامپیوتر است و از کنار هم قرار گرفتن بیت ها ساخته میشود تا داده های پیچیده تری را نمایش دهد.
مبنا ها در کامپیوتر و در منطق کامپیوتر:
- مبنای 2 ( باینری )
- مبنای 8 ( اکتال )
- مبنای 10 ( ده دهی )
- مبنای 16 (هگزادسیمال )
مبنای 2 یا باینری در منطق کامپیوتر چیست؟
مبنای 2 یا سیستم باینری یک سیستم عددی است که فقط از دو رقم 0 و 1 برای نمایش اعداد استفاده میکند. در حالی که ما انسان ها معمولا از مبنای 10 یعنی اعداد ۰0 تا 9 استفاده میکنیم، کامپیوتر ها با مبنای 2 کار میکنند چونکه مدار های الکترونیکی ان ها تنها دو حالت دارند 0 = خاموش، 1 = روشن. در این سیستم هر رقم یا بیت جایگاهی دارد که نمایانگر توان هایی از عدد 2 است.
یعنی انقدر عدد مورد نظر را بر 2 تقسیم میکنیم که باقیمانده 1 شود و از پایین به بالا خوانده میشود یعنی از باقیز مانده اخر به سمت باقی مانده اول باید نوشته شود. مثلا:عدد 21 که یک عدد ده دهی است انقدر بر 2 تقسیم میکنیم که با قیز مانده 1 شود و برابر با 10101 میشود. عدد باینری 1101 برابر است با مقدار ده دهی زیر است :
1*2⁰ + 0*2¹ + 1*2² + 1*2³ = 13
-
1 × 2⁰ = 1 × 1 = 1
-
0 × 2¹ = 0 × 2 = 0
-
1 × 2² = 1 × 4 = 4
-
1 × 2³ = 1 × 8 = 8
مبنای 2 زبان اصلی کامپیوتر ها hست و تمام اطلاعات دیجیتال در نهایت به صورت ترکیبی از صفر و یک در این سیستم نمایش داده میشود.
مبنای 8 یا اکتال در منطق کامپیوتر چیست؟
مبنای 8 یا سیستم اکتال یک سیستم عددی است که از هشت رقم 0 تا 7 برای نمایش اعداد استفاده میکند. در این سیستم هر رقم نشان دهنده توانی از عدد 8 است یعنی از راست به چپ به ترتیب: 1و 8و 64 و … مثلا عدد اکتال 157 برابر است با:
- 7 × 8⁰ = 7 × 1 = 7
- 5 × 8¹ = 5 × 8 = 40
- 1 × 8² = 1 × 64 = 64
- 64 + 40 + 7 = 111
- 157₈ = 111₁₀
پس 157 در مبنای 8 برابر با 111 در مبنای 10 است.
سیستم اکتال در گذشته در برنامه نویسی و سخت افزار کاربرد زیادی داشت، به دلیل اینکه هر رقم در مبنای 8 معادل دقیق 3 بیت 3 رقم باینری است. مبنای 8 پلی بین باینری یا مبنای2 و ده دهی یا مبنای 10 است. عدد باینری 11011 را میتوان به اکتال تبدیل کرد:
011 011 از راست به چپ سه تا سه تا جدا میکنیم ، 11011 → 011 011 ،
-
011₂ = 3₈
-
011₂ = 3₈
- 11011₂ = 33₈
مبنای 10 یا ده دهی در منطق کامپیوتر چیست؟
مبنای 10 یا سیستم ده دهی یا Decimal System همان سیستمی است که ما انسان ها در زندگی روز مره برای شمارشمان و محاسبه استفاده میکنیم. در این سیستم از ده رقم 0 تا 9 استفاده میشود، و هر رقم نشان دهنده توانی از عدد 10 است.
مثلا: در عدد 5247 اکتالا 8 داریم:
- 7 × 8⁰ = 7 × 1 = 7
- 4 × 8¹ = 4 × 8 = 32
- 2 × 8² = 2 × 64 = 128
- 5 × 8³ = 5 × 512 = 2560
- 2560 + 128 + 32 + 7 = 2727
- 5247₈ = 2727₁₀
پس ارزش هر رقم بستگی به جایگاه ان دارد که به این خصلت ارزش مکانی میگویند. مبنای 10 پایه ی اصلی محاسبات انسانی است، اما کامپیوتر ها از ان به طور مستقیم استفاده نمیکنند، داده ها را ابتدا به مبنای 2 تبدیل میکنند تا بتوانند ان را پردازش کنند.
مبنای 16 یا هگزادسیمال در منطق کامپیوتر چیست؟
مبنای 16 یا سیستم هگزادسیمال یک سیستم عددی است که از 16 رقم مختلف برای نمایش اعداد استفاده میکند. ارقام از 0 تا 9 و حروف A تا F یعنی (A , B , C, D , E , F) به کار میروند تا مقادیر 10 تا 15 را نشان دهند. هر رقم در مبنای 16 نشان دهنده توانی از عدد 16 است.
مثلا عدد هگزادسیمال 3F به مبنای 10 میشود:
- F × 16⁰ = 15 × 1 = 15 ( F = 15 در هگزادسیمال)
- 3 × 16¹ = 3 × 16 = 48
- 48 + 15 = 63
- 3F₁₆ = 63₁₀
مزیت مهم مبنای 16 این است که هر رقم ان دقیقا برابر با 4 بیت یعنی 4 رقم باینری است، پس برای نمایش داده های باینری بسیار مناسب است.
تبدیل عدد باینری 10101 که برابر عدد 21 ده دهی است به هگزادسیمال تبدیل کنید: ابتدا باید عدد را از سمت راست 4 تا 4 تا جدا کنیم ،الان در اینجا از راست به چپ 1010 0001 چون یک عدد باقی ماند باید به ازای 3 عدد دیگر 0 بگذاریم حالا اگر دو از سمت راست به چپ جدا میکردیم و 2 عدد میکاند باید 2 تا 0 میگذاشتیم که چهار تا تکمیل شود. جواب میشود 15.
- 1 0101
- 0001 0101
- 0001₂ = 1₁₆
- 0101₂ = 5₁₆
- 10101₂ = 15₁₆
تبدیل هگزادسیمال به اکتال در منطق کامپیوتر:
نمیشود مستقیم تبدیل کرد باید اول به باینری تبدیل کرد و بهد به اکتال یا هگزادسیمال تبدیل کنیم.
هگزادسیمال: F3 = F × 16¹ + 3 × 16⁰
تبدیل به باینری:
-
F₁₆ = 1111₂ :
F = 15 بنابراین برای تبدیل یک عدد دهدهی به باینری، جایگاههای توان 2 را در نظر میگیریم:
| توان 2 | 2³ | 2² | 2¹ | 2⁰ |
|---|---|---|---|---|
| مقدار | 8 | 4 | 2 | 1 |
-
3₁₆ = 0011₂
نتیجه :
- F3₁₆ = 11110011₂
- 11110011 → 001 111 001
- 001₂ = 1₈
- 111₂ = 7₈
- 001₂ = 1₈
- F3₁₆ = 171₈
جدول هگزادسیمال، معادل ده دهی و باینری 4 بیتی در منطق کامپیوتر:
| Hex | Decimal (دهدهی) | Binary (۴ بیتی) |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| A | 10 | 1010 |
| B | 11 | 1011 |
| C | 12 | 1100 |
| D | 13 | 1101 |
| E | 14 | 1110 |
| F | 15 | 1111 |
اهمیت تبدیل مبناها برای برنامه نویسی:
- آدرس دهی حافظه
- کار با رنگ ها در گرافیک ( Hex ) : RGB از صفر تا 255 یعنی هرکدام از R ، G و B یک بایت هستند و 0 تا 255 میزان شدت رنگ ها در هر پیکسل را نشان میدهد.
- فهم دستور العمل های ماشین
اینکدینگ در منطق کامپیوتر چیست؟
اینکدینگ چیست؟ Encoding در منطق کامپیوتر به معنای تبدیل داده ها از یک فرمت یا شکل به فرمت دیگری میباشد. هدف اصلی ان معمولا انتقال یا ذخیره سازی داده ها به شکل قابل استفاده برای سیستم های دیگر یا امن تر میباشد. به طور مثال:
-
تبدیل متن به باینری یا یونیکد UTF-8 تا کامپیوتر بتواند ان را ذخیره یا پردازش کند.
-
فشرده سازی فایل ها مانند ZIP کردن.
-
تبدیل داده ها به Base64 برای ارسال در ایمیل یا شبکه ها.
اینکدینگ مثل رمز گذاری داده برای قابل انتقال شدن است، ولی لزوما امنیتی نیست برخلاف رمزنگاری.
دیکدینگ در منطق کامپیوتر چیست؟
دیکدینگ یا Decoding چیست؟ دیکدینگ دقیقا برعکس اینکدینگ میباشد. داده های اینکد شده را به شکل اصلی یا قابل فهم برای انسان یا برنامه برمیگرداند. به طور مثال:
-
تبدیل متن UTF-8 به کاراکتر های قابل خواندن.
-
باز کردن فایل ZIP.
-
تبدیل Base64 به فایل اصلی.
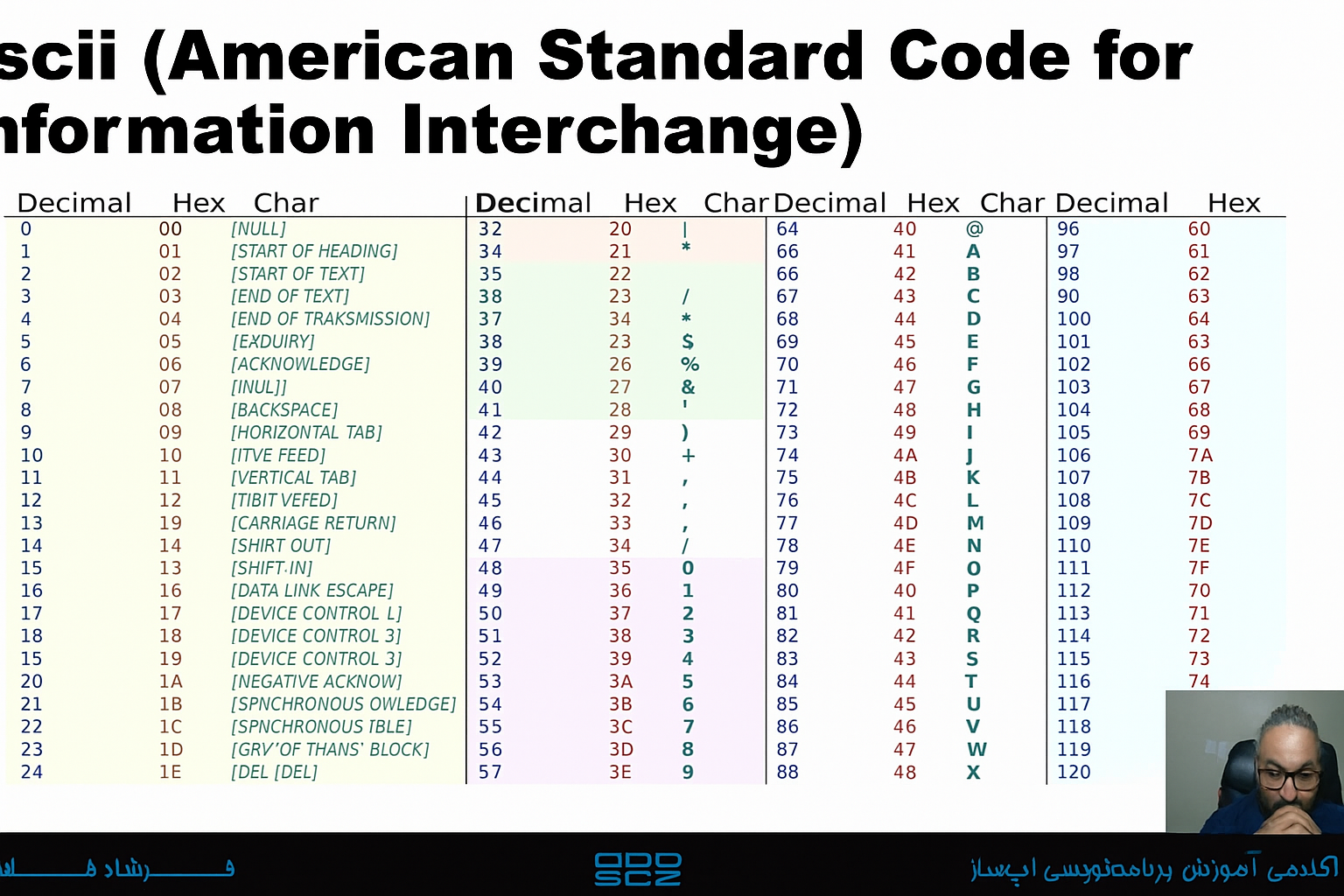
کد ASCII یکی از قدیمی ترین و معروف ترین استاندارد های اینکدینگ است.
کد ASCII چیست در منطق کامپیوتر چیست؟
ASCLL در منطق کامپیوتر به معنی تبدیل کاراکتر های قابل چاپ و کنترل مانند: حروف، اعداد و علائم به اعداد باینری. ویژگی های کد ascll شامل : فقط شامل 128 کاراکتر پایه 0 تا 127 است. زبان ها و نماد های غیر انگلیسی را پشتیبانی نمیکند. هنوز هم پایه خیلی از استاندارد های جدید مثل UTF-8 میباشد. اما یک مشکل داشت اینکه کامل نبود و بخاطر همین یونیکد را بوجود اوردند.
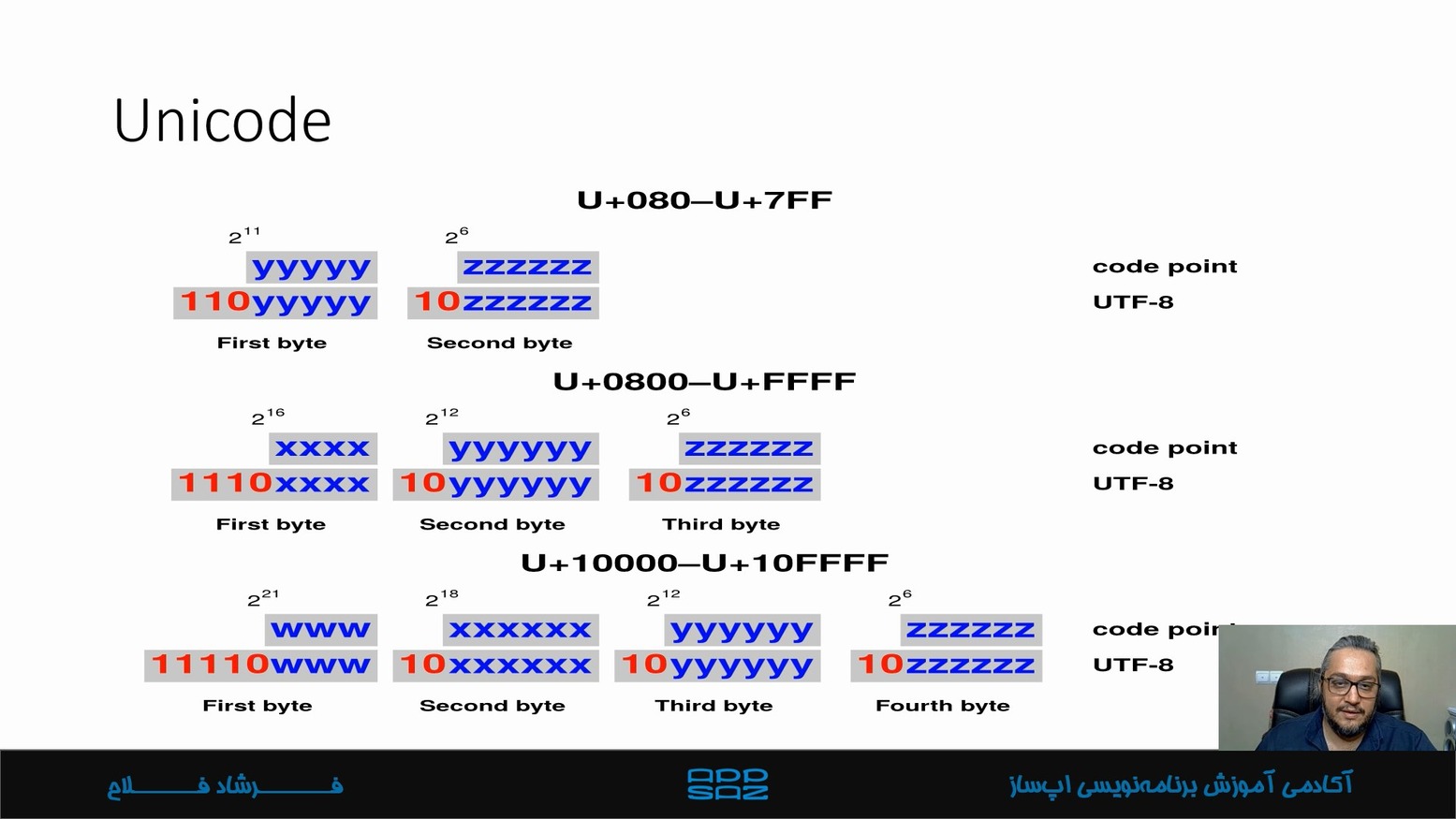
یونیکد Unicode در منطق کامپیوتر چیست؟
یونیکد در منطق کامپیوتر یک استاندارد جهانی برای نمایش و پردازش متن ها از تمام زبان ها و نماد های دنیا میباشد. قبل از یونیکد، هر زبان یا سیستم کامپیوتری معمولا کد گذاری خودش را داشت مثل ASCII یا ISO 8859-1 و این باعث مشکلات بزرگی در انتقال متن بین سیستم ها میشد. ویژگی های یونیکد شامل: پشتیبانی از تمام زبان ها مثل: انگلیسی، فارسی، چینی، عربی، ژاپنی و حتی اموجی های مختلف. تعیین یک عدد یکتا برای هر کاراکتر هر کاراکتر یک کد نقطه ای code point دارد.
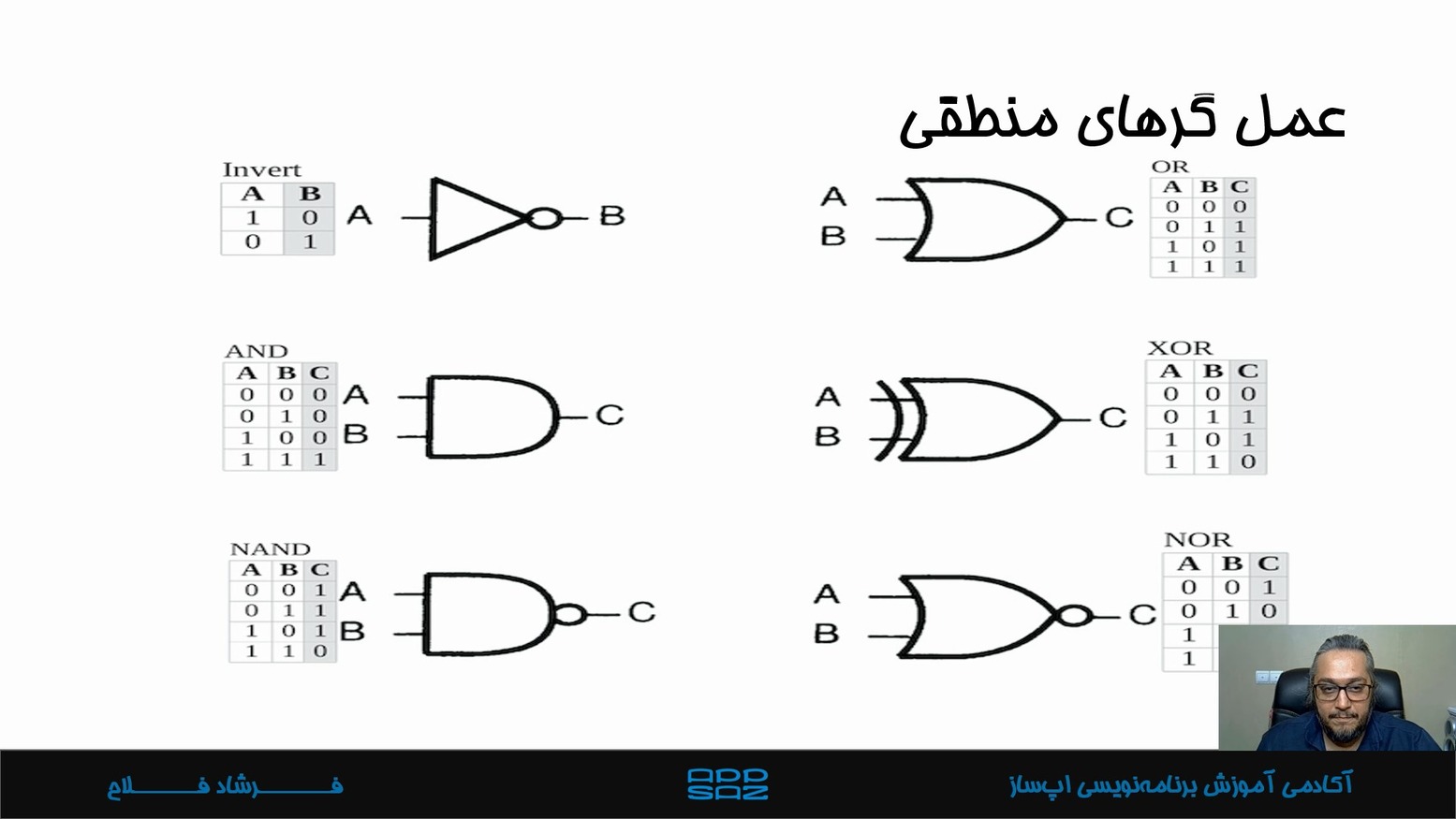
عملگر های منطقی در منطق کامپیوتر،جبر بولی و عملگر ها:
منطق کامپیوتر با جبر بولی کار میکند. در جبر بولی، همه چیز به دو حالت محدود میشود درست (۱) و غلط (۰) و عملگر های اصلی شامل موارد زیر است:
-
AND و
-
OR یا
-
NOT نفی
-
XOR (Exclusive OR ، یا انحصاری)
-
NAND (Not AND، یا نفی AND)
-
NOR (Not OR ، یا نفی OR)
-
XNOR (Exclusive NOR، یا برابری منطقی)
-
AND (و)
نماد ان به صورت مقابل است.( && یا and ) . نتیجه درست است فقط وقتی که هر دو شرط درست باشند. کاربرد ان بررسی هم زمان چند شرط، مثل اجازه ورود به کاربر فقط اگر رمز صحیح و نام کاربری صحیح باشد. جدول درستی به شکل زیر است:
| A | B | A AND B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | False |
-
OR (یا)
نماد ان به صورت ( || یا Or ) است. نتیجه درست است اگر حداقل یکی از شرط ها درست باشد. وقتی شرط کافی است که یکی از شرایط برقرار باشد، به طور مثال: دسترسی به کاربر اگر مدیر باشد یا VIP باشد. جدول درستی انن به شکل زیر است:
| A | B | A OR B |
|---|---|---|
| True | True | True |
| True | False | True |
| False | True | True |
| False | False | False |
-
NOT (نفی)
نماد ان به شکل ! یا not است. نتیجه برعکس شرط است. زمانی که میخواهیم شرط برعکس حالت باشد، به طور مثال: اجازه ورود اگر کاربر مسدود نشده باشد.
جدول درستی:
| A | NOT A |
|---|---|
| True | False |
| False | True |
-
XOR (Exclusive OR)
نماد ان به صورت ^ یا XOR است. نتیجه درست است اگر دقیقا یکی از شرط ها درست باشد. وقتی میخواهیم فقط یکی از دو شرط برقرار باشد، به طور مثال: روشن بودن چراغ قرمز یا سبز، ولی نه هر دو با هم. جدول درستی ان به شکل زیر است:
| A | B | A XOR B |
|---|---|---|
| True | True | False |
| True | False | True |
| False | True | True |
| False | False | False |
-
NAND (Not AND)
نماد ان به شکل ! (A AND B) است. نتیجه برعکس AND است. در مدار های دیجیتال، یکی از پایه ای ترین گیت ها است. جدول درستی به شکل زیر است:
| A | B | A NAND B |
|---|---|---|
| True | True | False |
| True | False | True |
| False | True | True |
| False | False | True |
-
NOR (Not OR)
نماد ان به صورت ! (A OR B) است. نتیجه برعکس OR است. در مدار های دیجیتال و بعضی الگوریتم ها برای زمانی که هیچ شرطی نباید برقرار باشد. جدول درستی ان به شکل زیر است:
| A | B | A NOR B |
|---|---|---|
| True | True | False |
| True | False | False |
| False | True | False |
| False | False | True |
-
XNOR (Exclusive NOR)
نماد ان به صورت ! (A XOR B) است. نتیجه درست است اگر هر دو شرط مشابه باشند یعنی هر دو درست یا هر دو غلط باشند. بررسی برابری منطقی دو شرط، به طور مثال: رمز وارد شده با رمز ذخیره شده یکی باشد. جدول درستی ان به شکل زیر است:
| A | B | A XNOR B |
|---|---|---|
| True | True | True |
| True | False | False |
| False | True | False |
| False | False | True |
-
AND: هر دو باید درست باشند تا نتیجه درست شود.
-
OR: حداقل یکی درست باشد نتیجه درست است و اما اگر هر دو غلط باشند نتیجه غلط است.
-
NOT: معکوس
-
XOR: فقط یکی درست باشد نتیجه درست است اما اگر هر دو درست یا هر دو غلط باشند نتیجه غلط میباشد.
-
NAND: NOT AND شرط اول درست شرط دوم درست نتیجه غلط میشود و برعکس . و همینطور اگر یکی از شرط ها درست دیگری غلط باشد نتیجه درست است.
-
NOR: NOT OR شرط اول درست و شرط دوم درست نتیجه غلط میشود و اکر هر دو شرط غلط باشند نتیجه درست میباشد و همچنین یک شرط درست و دیگری غلط نتیجه غلط میشود.
-
XNOR: معادل بودن یا هر دو درست یا هر دو غلط نتیجه درست است. یکی غلط و دیگری درست نتیجه غلط میباشد.
Half Adder جمع کننده نیمه کامل در منطق کامپیوتر چیست؟
Half Adder جمع کننده نیمه کامل در منطق کامپیوتر یعنی جمع دو بیت یعنی دو رقم باینری بدون در نظر گرفتن حمل Carry قبلی. ورودی ها و خروجی ها شامل: ورودی ها: A و B دو بیت برای جمع خروجی ها:
- Sum یا جمع: نتیجه جمع A و B
- Carry یا حمل: در صورتی که جمع > 1 شود به طور مثال 1+1=10 در باینری ، این بیت فعال میشود.
جدول درستی ان به صورت زیر است:
| A | B | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
روابط منطقی ان به صورت زیر است:
-
Sum = A XOR B
-
Carry = A AND B
چون Half Adder فقط دو بیت را جمع میکند و حمل قبلی را نمیتواند لحاظ کند، محدود است.
Full Adder یا جمع کننده کامل در منطق کامپیوتر چیست؟
Full Adder یا جمع کننده کامل در منطق کامپیوتر یعنی جمع دو بیت به همراه حمل قبلی Carry in. برای جمع زنجیره ای در مدار های چند بیتی استفاده میشود. ورودی ها و خروجی های ان به این صورت است که: ورودی ها: A،B،Cin حمل ورودی. خروجی ها:
- Sum یا جمع
- Cout یا حمل خروجی
جدول درستی ان به صورت زیر است:
| A | B | Cin | Sum | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
روابط منطقی ان به شکل زیر میباشد:
-
Sum = A XOR B XOR Cin
-
Cout = (A AND B) OR (B AND Cin) OR (A AND Cin)
Full Adder قابل ترکیب برای جمع چند بیتی است، یعنی میتوان چند Full Adder را کنار هم گذاشت تا یک جمعکننده 4 بیتی، 8 بیتی و … ساخت.
| ویژگی | Half Adder | Full Adder |
|---|---|---|
| ورودیها | ۲ (A و B) | ۳ (A، B، Cin) |
| خروجیها | Sum و Carry | Sum و Cout |
| قابلیت | جمع دو بیت بدون حمل | جمع دو بیت با حمل قبلی |
| استفاده | ساده، محدود | جمع چندبیتی زنجیرهای |
جدول های صحت یا Truth Tables در منطق کامپیوتر:
در منطق کامپیوتر برای هر ترکیب ورودی، خروجی منطقی مشخص میشود. جدول های صحت ابزار مهمی برای طراحی و بررسی مدار ها و الگوریتم ها هستند.
منطق فازی و غیر قطعی در منطق کامپیوتر:
در دنیای واقعی، اطلاعات همیشه قطعی نیستند. در منطق کامپیوتر بخش منطق فازی این امکان را میدهد که سیستم ها با داده های مبهم یا نسبی هم کار کنند، مثل تشخیص دما یا ریسک مالی.
نتیجه گیری:
منطق کامپیوتر پایه و اساس تمام محاسبات دیجیتال و الگوریتم ها را تشکیل میدهد. با استفاده از گزاره ها، عملگر ها و جبر بولی، میتوان رفتار سیستم های پیچیده را مدل سازی کرد. منطق شرطی و قیاسی امکان طراحی مدار ها و برنامه های کار امد را فراهم میکند. طراحی سخت افزار بدون درک عمیق منطق، امکان پذیر نیست و خطا های جدی ایجاد میکند. به کمک جدول های صحت و قضایای منطق، صحت برنامه ها و مدار ها قابل اثبات میباشد.
منطق فازی و غیر قطعی، توانایی پردازش داده های غیر شفاف و واقعیت های پیچیده را به کامپیوتر میدهد. یاد گیری ماشین و هوش مصنوعی نیز بر پایه اصول منطقی و قوانین تصمیم گیری استوار میباشد. تقویت مهارت های منطقی باعث بهبود تحلیل مسئله و حل مسائل پیچیده میشود. منطق کامپیوتر نه تنها ابزار محاسباتی، بلکه چهار چوبی برای تفکر دقیق و سیستماتیک در علوم کامپیوتر میباشد.